Search and install the plugin using the Extension Manager. Refer to Plugins on how to install plugins manually.

Please report bugs or feature requests at the Bug tracker.

• Git Repository
• Bug Tracker

• Update plugin.info.txt (2023/08/18 14:14)
• Clean up code (2023/08/18 14:12)
• Merge pull request #17 from Miro-Collas/master (2023/08/18 14:11)
• Update syntax.php (2023/08/18 03:19)
• Upped version. (2016/04/26 22:02)
• Merge pull request #10 from splitbrain-forks/php7-signature (2016/02/27 23:32)
• Adjust method signatures to match parent (2016/02/02 18:03)
• replaced VERSION/getinfo() by plugin.info.txt (2010/11/22 18:43)

• Email address is wrong
• This doesn't work on 2013-12-08 «Binky»
• Does not filter out comments within data plugin entries - they are shown. Bugreport
• For the current Dokuwiki version, use the 'comment syntax' plugin
  • Which version is meant with 'current Dokuwiki'? The 'comment' plugin is marked as 'compatible' for Frusterick Manners (which is the current version as of the writing of this question), while 'comment syntax' is marked as 'probably' — Dralli72 2018-03-07 00:43

Высокая проводимость металлов обусловлена наличием в них электронов проводимости, образующих электронный газ. Для оценки можно считать, что каждый из атомов металлов, образующих кристаллическую решетку, «отдает» в электронный газ несколько электронов (обычно от одного до трех в зависимости от типа металла). Эти электроны уже не принадлежат ионам решетки, а являются «общими» для всего объема металла. При включении металлического проводника в электрическую цепь электроны проводимости перемещаются, обеспечивая соответствующий ток проводимости. Поскольку плотность металлов составляет примерно $10^{28\div29}$ $\frac{{атомов}}{{м}^{3}}$, то концентрация (плотность) электронного газа очень высока. Это и объясняет высокую электропроводность металлов.

Хотя электроны проводимости ведут себя в металле во многих отношениях подобно газу (могут свободно перемещаться по всему объему металла, их плотность испытывает тепловые флуктуации; что обуславливает так называемый тепловой шум, и т.п.), но, чтобы выйти за пределы объема металла, они должны совершить определенную работу, называемую работой выхода. Если эта работа совершается за счет нагрева металла, то процесс выхода электронов из металлов называется термоэлектронной эмиссией.

Силы, по преодолению которых эмитированные электроны должны совершить работу выхода, в простейшей модели (классическая модель Шоттки) описываются двумя компонентами: двойным электрическим слоем на границе металла с вакуумом и силами «изображения» (рис. 2).

В отсутствие внешних полей электронный газ «распространяется» за поверхность металла на расстояния $x_{0}$ порядка межатомных, и в этом поверхностном слое (его называют двойной слой) на электрон действует некоторая сила $F_{0}$. Можно считать, что двойной слой образует «плоский конденсатор», внешняя обкладка которого заряжена отрицательно. Поэтому силу $F_{0}$ можно принять постоянной $F_{0}=eE$ (рис. 2, в), где величина $E$ (напряженность поля двойного слоя) зависит от плотности электронного газа и различна для разных металлов. Когда электрон уходит на расстояния больше $x_{0}$, металл в целом оказывается положительно заряженным, и действующую на электрон силу можно определить как силу Кулона между электроном ($-e$) и его «зеркальным изображением» ($+e$) (см. рис. 2, б):

$F_{im}=-\frac{e^{2}}{4x^{2}}$, дин (СГС) или $F_{im}=-\frac{e^{2}}{16\pi\varepsilon_{0}x^{2}}$, Н (СИ)

В точке $x_{0}$ эти силы должны «сшиваться» по величине, что помогает определить величину силы $F_{0}$:

$F_{0}=\left.F_{im}\right|_{x_{0}}=-\frac{e^{2}}{4x_{0}^{2}}$, дин (СГС) или $F_{0}=\left.F_{im}\right|_{x_{0}}=-\frac{e^{2}}{16\pi\varepsilon_{0}x_{0}^{2}}$, Н (СИ)

Общая работа сил, затрачиваемая на выход электрона из металла, определится интегрированием по всему пространству вдоль направления $x$ от $0$ до $\infty$:

$$ W_{p}=\int_{0}^{\infty}F(x)dx=\frac{e^{2}}{4x_{0}}+\int_{x_{0}}^{\infty}\frac{e^{2}}{4x^{2}}dx=\frac{e^{2}}{2x},\text{ эрг }(\text{СГС})\label{eq:1} $$ или $W_{p}=-\frac{e^{2}}{8\pi\varepsilon_{0}x_{0}}$, Н (СИ), где $e=1,6\cdot10^{-19}$ Кл — заряд электрона; $\varepsilon_{0}=8,85\cdot10^{-12}$ $\frac{{Ф}}{{м}}$ — электрическая постоянная (диэлектрическая проницаемость вакуума).

Величина работы выхода $W_{p}$ рассчитана исходя из классических соображений. Она называется полной работой выхода. Реальные работы выхода $W_{a}$, измеряемые в экспериментах по термоэмиссии, оказались заметно меньше по величине. Это различие было объяснено на базе квантовой физики.

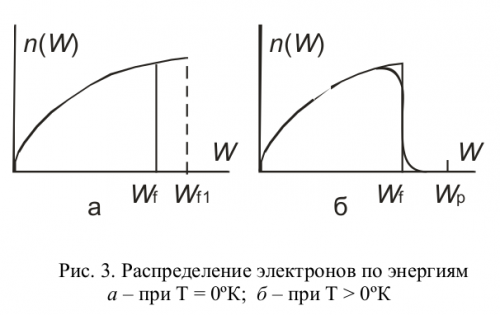
Суть объяснения заключается в следующем. Плотность электронного газа в металле весьма высока. Поэтому электроны проводимости нельзя считать ``свободными'' в классическом смысле слова. Они представляют единую квантовую систему. Согласно квантовым законам даже при абсолютном нуле температуры все электроны системы не могут иметь одинаковую — нулевую — энергию, поскольку в соответствии с квантовым запретом Паули в одном квантовом состоянии (с данной энергией) может находиться не более двух электронов, отличающихся проекцией спина. Распределение электронов квантовой системы по энергиям в этом случае описывается статистикой Ферми– Дирака.

На рис. 3 изображен вид этого распределения для двух значений температуры: $T=0^{\circ}\:{К}$ и $T>0^{\circ}\:{К}$. Максимальная энергия $W_{f}$ при $0^{\circ}\:{К}$ называется уровнем Ферми (энергией Ферми, химическим потенциалом идеального электронного газа).

Поскольку при термоэмиссии металл покидают наиболее энергичные электроны, имеющие энергию, близкую к энергии Ферми, то можно считать, что для выхода им достаточно затратить лишь часть необходимой энергии, равной разнице между $W_{p}$ и $W_{f}$:

Здесь $e>0$ — элементарный заряд, а $W$ и $e\varphi$ — работа выхода в Дж (СИ). Ее также часто выражают в электрон–вольтах (эВ). Внесистемная единица (электрон-вольт) широко принята в практике. Так 1 эВ — это работа (энергия), которую приобретает электрон, пройдя без соударения разность потенциалов в 1 В. Чтобы пересчитать работу выхода из эВ в единицы СИ или СГС, нужно умножить это значение на заряд электрона в соответствующей системе единиц ($1\:{эВ}=1,6\cdot10^{-19}\text{ Дж}$).

\begin{comment} Следует отметить, что в разных научных школах для указания работы выхода приняты разные, отчасти противоречивые обозначения. В одних работа выхода обозначается через A, или W и e , как это сделано выше, а в других — через символ , который, как и символ U, также обычно используется для обозначения потенциала. Мы не будем изменять сложившиеся традиции и в необходимых местах будем делать соответствующие уточнения. \end{comment}

Величина энергии Ферми в металле $W_{f}$ зависит только от концентрации электронов проводимости (от плотности электронного газа) и равна $$ W_{f}=\frac{h^{2}}{2m}\left(\frac{3n}{8\pi}\right)^{\frac{2}{3}},\text{ Дж,}\label{eq:3} $$ где $n$ — концентрация, $\lyxmathsym{м}^{3}$; $m=9,1\cdot10^{-31}\text{ кг}$ — масса электрона; h — постоянная Планка: $h=6,63\cdot10^{-34}\text{ Дж}\cdot\text{с}$.

Для различных металлов плотность электронного газа различна, поэтому различен и уровень Ферми. Пунктиром на рис. 3,~а показан уровень Ферми $W_{f1}$, соответствующий металлу с большей плотностью электронного газа, чем у металла, характеризуемого сплошной линией. По порядку величины уровень (энергия) Ферми для всех металлов примерно одинаков и составляет несколько эВ (табл. 1). \begin{table} \begin{centering} \begin{tabular}{|c|c|c|c|} \hline Металл & $n\cdot10^{-28}$, $\text{м}^{3}$ & $W_{f}\cdot10^{19}$, Дж & $\varphi,$ эВ\tabularnewline \hline \hline Th & & 5,28 & 3,3\tabularnewline \hline K & 1,33 & 3,55 & 2,22\tabularnewline \hline Cu & 8,4 & 7,04 & 4,4\tabularnewline \hline Ag & 5,9 & & 4,3\tabularnewline \hline W & 6,3 & 7,26 & 4,54\tabularnewline \hline Ni & & 7,2 & 4,5\tabularnewline \hline \end{tabular} \par\end{centering}

\begin{centering} Таблица 1. \par\end{centering}

\begin{centering} Концентрация электронов проводимости $n$, уровни \par\end{centering}

\centering{}Ферми $W_{f}$ и работа выхода различных металлов \end{table}